MATEMATIKA SMP: 1. Bil. Berpangkat dan Akar

(Pertemuan ke-1)

A.Bilangan Rasional Berpangkat Bilangan Bulat
1.Bilangan Rasional.
Bilangan rasional adalah bilangan yang dapat dinyatakan dalam bentuk 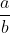$\frac{a}{b}$ , dengan a dan b adalah bilangan bulat serta b $\displaystyle \neq$ 0.
Contoh bilangan rasional ; $\frac{2}{3} , -\frac{10}{2} , \sqrt{9}$

2.Pengertian Bilangan Rasional Berpangkat Bilangan Bulat Positif
Jika a bilangan rasional dan n bilangan bulat positif maka perkalian berulang n faktor dari a ialah:

3. Sifat Bilangan Rasional Berpangkat Bilangan Bulat
Jika m, n, p dan q adalah bilangan bulat, maka :

1.   $p^{m}\times p^{n}=p^{m+n}$
2.   $p^{^{m}} : p^{^{n}} = p^{^{m-n}}$
3.   $(p^{m})^{n} = p^{m\times n }$
4.   $(p\times q)^{m} = p^{m}\times q^{m}$
5.   $(\frac{p}{q})^{m} = \frac{p^{m}}{q^{m}}$
6.   $pa^{m} + qa^{n}= a^{m}(p+qa^{m-n}), jika: m > n$
7.   $pa^{m} - qa^{n}= a^{m}(p-qa^{m-n}), jika: m > n$

Latihan Soal 1.1.
Tentukan hasil dari operasi hitung berikut dengan menggunakan sifat-sifat bilangan rasional berpangkat.
1. $(-3)^{^{-3}}\times (-3)^{^{8}} = ...$

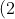2. $(2)^{^{-3}} + (2)^{^{4}} -(2)^{^{2}} = ...$

3. $\frac{12a^{3}}{a^{5}} = ...$

4. $12a^{3}:{2a^{-5}} = ...$

5. $(\frac{2}{3})^{3} \times (\frac{2}{3})^{} \times (\frac{2}{3})^{-2} = ....$

6. $(\frac{3}{4})^{2}\div (\frac{3}{4})^{5} \times (\frac{3}{4})^{-4} = ....$

7. $(\frac{2}{5})^{-1}\times (\frac{5}{2})^{2} = ....$

8. Tentukan nilai k jika 3^k = 729

9. Tentukan nilai n jika 96 : 3 = n⁵

10. Benda jatuh dari atas gedung tanpa memiliki kecepatan awal. Tinggi gedung dirumuskan h = v₀.t + ½gt², dengan h= tinggi gedung dan t = waktu. Jika benda menyentuh tanah dalam waktu 3 sekon dan gravitasi bumi (g) 10 m/s², berapakah ketinggian gedung itu?

(Pertemuan ke-2)

B. Bilangan Rasional Berpangkat Bilangan Bulat Negatif dan Nol

Pengertian Pangkat Bilangan Bulat Negatif dan Nol.

Telah kita pelajari bahwa jika a adalah bilangan rasional, a≠0, dan p, q adalah bilangan bulat positif dengan p > q, maka :

$\frac{a^{p}}{a^{q}} = a^{p-q}$ maka :

$\frac{a^2}{a^5}=a^{2-5}=a^{-3}=\frac{a\times a}{a\times a\times a\times a\times a}=\frac{1}{a^3}$

$\frac{a^3}{a^3}=a^{3-3}=a^{0}=\frac{a\times a\times a}{a\times a\times a}=1$

$\left ( \frac{a}{b} \right )^{-n}=\frac{1}{\left ( \frac{a}{b} \right )^{n}}=\frac{1}{\frac{a^n}{b^n}}=1\div\frac{a^n}{b^n}=1\times\frac{b^n}{a^n} = \left ( \frac{b}{a} \right )^{n}$

Sehingga didapatkan sifat perpangkatan :

1. $a^{-n}= \frac{1}{a^n}$
2. $a^{0}= 1$
3. $\left ( \frac{a}{b} \right )^{-n}=\left ( \frac{b}{a} \right )^{n}$

Latihan Soal 1.2.
Tentukan hasil dari operasi hitung berikut dengan menggunakan sifat-sifat bilangan rasional berpangkat.
1. Tentukan hasil dari :
a. 3²+ 3^-2
b. (-3)³+ (-3)² + (-3)¹+ (-3)⁰

2. Tentukan hasil dari :

a. 2+ 2^-2x 2⁵x 2^-1
b. (-2)³x (-2)² x (-2)¹x (-2)⁰

3. Tentukan hasil dari 4 - 5^-4 x 5³

4. Tentukan hasil dari (-3)³x (-3)² + (-3)¹+ (-3)⁰- (-3)^-1

$5. \left ( \frac{2}{5} \right )^{5}\times \left ( \frac{2}{5} \right )^{-2} =$
$6. \left (- \frac{3}{2} \right )^{1}\div \left (- \frac{3}{2} \right )^{4} =$
$7. \left (- \frac{1}{2} \right )^{2}\times \left (- \frac{1}{2} \right )^{-3} =$

8. Tentukan nilai x jika 25^x+4= 1
$9. \frac{4^{1011}-4^{1010}}{2^{2020}-2^{2019}} =$
10.

Sebuah benda yang terbuat dari baja memiliki panjang 1000 cm. Berapakah pertambahan panjang baja itu, jika terjadi perubahan suhu sebesar 50°C?

(Rumus : L = L0(1 + α∆T) dan koedisien muai panjang baja α = 12 × 10-6)

MATEMATIKA SMP

HALAMAN

Sabtu, 04 Juli 2020

1. Bil. Berpangkat dan Akar

Tidak ada komentar:

Posting Komentar